트리 자체는 기존에 찾아봤었다. 하지만 내용도 많고 종류도 많아서 이런 형태구나 하는 정도만 알고 넘어갔다. 그러다 이번에 이진트리에 대해서 보다 자세히 찾아봤다.
이진트리란 모든 노드들이 둘 이하의 자식을 가진 트리이다.
이진트리의 순회
이진트리 순회 알고리즘은 트리에 저장된 모든 노드를 빠짐없이 살펴보고 싶을 때 사용한다. 깊이 우선 순회 방법으로는 전위 순회, 중위 순회, 후위 순회 가 있고, 너비 우선 순회 방법으로는 레벨 순회 가 있다.

- 전위 순회(pre-order): NLR
- 중위 순회(in-order): LNR
- 후위 순회(post-order): LRN
- 레벨 순회(level-order): NLR

- 전위 순회(pre-order): 1 2 4 5 3 6 7
- 중위 순회(in-order): 4 2 5 1 6 3 7
- 후위 순회(post-order): 4 5 2 6 7 3 1
- 레벨 순회(level-order): 1 2 3 4 5 6 7
이진트리의 종류
이 외에도 많은 종류가 있지만 대표적인 것들 몇 개만 소개한다.
완전 이진트리(Complete Binary Tree)
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
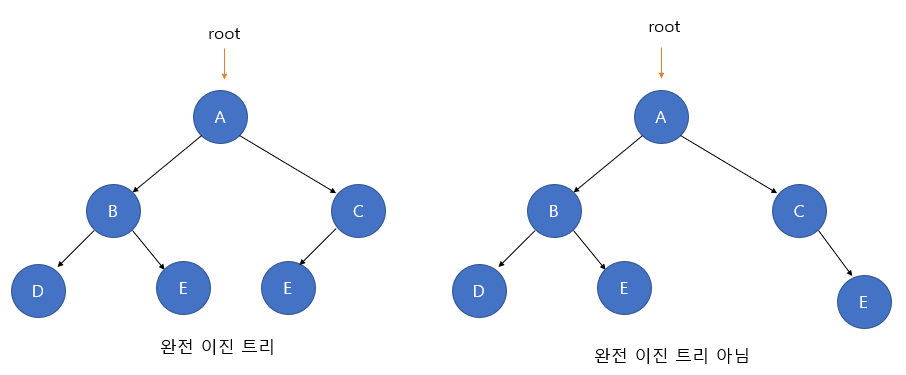
- 마지막 레벨은 꽉 차 있지 않아도 되지만, 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
- 트리의 높이가 h일때 2^(h-1) ~ 2^h-1 개의 노드를 가질 수 있다.
- 완전 이진 트리는 배열을 사용해 효율적으로 표현 가능하다.
전 이진트리(Full Binary Tree)
모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.

포화 이진트리(Perfect Binary Tree)
모든 레벨이 노드로 꽉 차 있는 트리를 뜻한다.
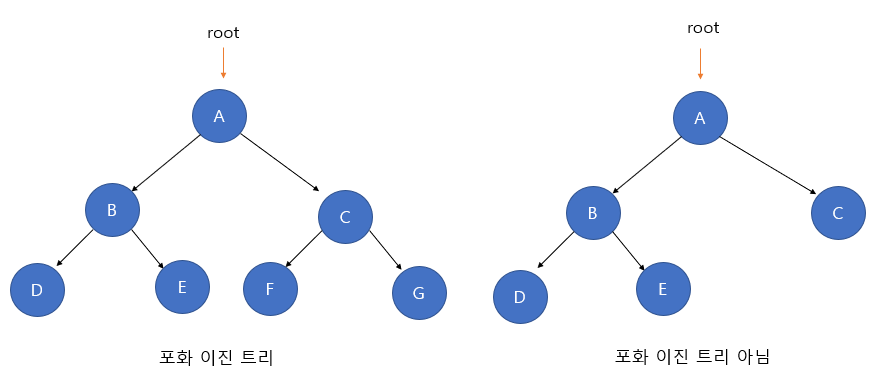
- 전 이진트리의 성질도 만족해야 한다. 즉, 모든 노드가 0개 혹은 2개의 자식 노드를 갖는다.
- 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
- 트리의 노드 개수가 정확히 2^k-1 개여야 한다. 여기서 k는 트리의 높이다.
이진탐색트리(Binary Search Tree)
기존 이진트리보다 탐색이 빠르다. 이진 탐색 트리의 탐색 연산은 트리의 높이(height)가 h라면 O(h)의 시간 복잡도를 갖는다.

- 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.
- 부모의 키가 왼쪽 자식 노드의 키보다 크다.
- 부모의 키가 오른쪽 자식 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
- 이진 탐색 트리는 효율적인 탐색을 위해 고안된 트리이다.
이진 탐색 트리 구현
// 이진탐색트리 (Binary Search Tree)
class treeNode {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class insertNode {
constructor() {
this.root = null;
}
insert(data) {
let node = new treeNode(data);
// 루드가 설정되어 있지 않다면 루트를 node로 만들어 준다. node는 treeNode()에서 뼈대를 받아온다.
if (!this.root) {
this.root = node;
return this;
}
// 비교를 위해 current 를 설정해 준다.
let current = this.root;
// current가 true 라면 while문을 돌면서 data와 지금 현재 data인 current data를 비교한다.
while (current) {
// 중복된 값은 어떤 결과를 리턴하지 않는다.
if (data === current.data) {
return;
}
// data가 current data(기준) 보다 작다면 왼쪽에 넣어준다.
if (data < current.data) {
if (!current.left) {
current.left = node;
break;
}
// 이제 current data(기준)는 왼쪽의 data로 준다.
current = current.left;
}
// data가 기준 data(current data) 보다 크다면 오른쪽에 넣어준다.
if (data > current.data) {
if (!current.right) {
current.right = node;
break;
}
// 이제 current data(기준)는 오른쪽 data로 준다.
current = current.right;
}
}
}
find(data) {
let current = this.root;
while (current) {
if (current.data === data) {
return current;
}
if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return null;
}
}
let nums = new insertNode();
nums.insert(10);
nums.insert(5);
nums.insert(11);
nums.insert(3);
nums.insert(6);
console.log(nums)
// insertNode {
// root: treeNode {
// data: 10,
// left: treeNode { data: 5, left: 3, right: 6 },
// right: 11
// }
// }
let foundNode = nums.find(6);
if (foundNode !== null) {
console.log("Node found:", foundNode);
} else {
console.log("Node not found");
}
//! 중복값 허용 안됨
//! insert 메서드에서 this는 호출한 객체 즉 클래스를 가리킨다.
아직은 내가 직접 구현하기보다는 누군가 만든 것을 뜯어서 어떻게 돌아가지 하며 이해하는 수준이다. 하지만 이렇게 꾸준히 하다 보면 언젠가 자연스럽게 내가 생각한 것들을 구현할 수 있게 될 것이라 믿는다. 이진트리만 해도 이 외에 더 많은 내용이 있지만 우선 이진 탐색 트리만이라도 알고 가는 게 좋아 보인다.
참고
https://code-lab1.tistory.com/8
https://ukcasso.tistory.com/11
'오늘 뭐했냐 > 개발에 대한 주저리' 카테고리의 다른 글
| 23.09.17 힙 더 알고 가자 (0) | 2023.09.19 |
|---|---|
| 23.09.16 우선순위 큐(Priority Queue) (0) | 2023.09.18 |
| 23.09.14 인덱스(index) (0) | 2023.09.17 |
| 23.09.13 시간 복잡도와 공간 복잡도 (0) | 2023.09.16 |
| 23.09.12 오버로딩 오버라이딩 (0) | 2023.09.15 |